There are many different shapes. There might seem to be hundreds of different shapes and you could try to learn them all but:
This is confusing
This is a waste of time
This is pointless. We need to see what they have in common and what is different about them.
It is much better to concentrate on the properties of shapes. This way you can remember a few facts and them use them to find out more about different shapes.
The 3 properties of shapes that we are going to look at are:
The number of sides
The interior angles (the angles inside).
The length of the sides.
These properties help use to remember which shapes are which and why they are so called (in some cases).
Let's start with a shape that has 3 sides: TRIANGLES (tri- means 3).
Triangles ALWAYS
have 3 sides.
The interior angles of a triangle add up to 180 degrees.
Here are the triangles you are expected to know about:
Equilateral Triangle
Isosceles Triangle
Right- Angled Triangle
Scalene Triangle
That doesn't seem too many does it? Let's look at the properties of triangles.
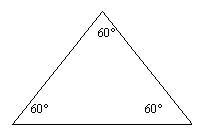
Equilateral Triangle
An equilateral triangle has got 3 sides of equal length and 3
angles that are equal.
Since ALL the angles in a triangle add up to 180º then 180 divided by 3 must be
60º.

The clue is in the name EQUILateral.
So if the length of one of the sides is 8 cm what is the combined length of
the other two sides?
The answer is 16 cm because 8cm is the length of one side of an equilateral triangle, then each other side must be 8cm. So 8 cm + 8cm = 16cm.
That is an easy triangle. Let's look at another one.
Isosceles Triangle
An Isosceles triangle has got two sides of equal length and 2 angles equal.
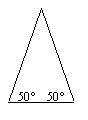
What is the value of the angle at the
top of this Isosceles triangle?
Answer
The answer is 80˚. All angles in a triangle add up to 180˚ so 180 - (50+50) = 80˚
So an isosceles triangle has only got two sides of equal length and two angles the same.
What about another triangle?
Right- Angled Triangle
The right angled triangle contains a right angle (an angle of 90˚)

In a right angled triangle what must the other two angles add up to?
90˚. Do you know why?
Because all the angles in a triangle add up to 180˚ and a Right Angled Triangle has got one angle of 90˚.
Well, there is only one more triangle to go
Scalene Triangle
A scalene triangle is the easiest of them all. The scalene triangle has got NO sides of equal length and NO angles the same.
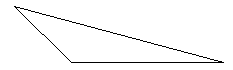
But it is a triangle. Can you think of the two reasons why?
Because its inside (interior) angles add up to 180.
Because it has got 3 sides.
Okay that wasn't so bad was it? Let's review what you have revised today.
There are 4 types of triangle. Each of these has got different properties in the number of sides of same length and the number of equal angles.
Look at the names below and see if you can remember what properties that they have. When you have thought about all four click on "check your answers" and see if you were right.
Isosceles Triangle
Right- Angled Triangle
Here are the things to remember
An equilateral triangle has got 3 sides of equal length and 3 angles that are equal.
An Isosceles triangle has got two sides of equal length and 2 angles equal.
The right-angled triangle contains a right angle (an angle of 90˚)
The scalene triangle has got NO sides of equal length and NO angles the same.