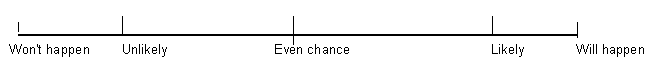
Probability - Introduction
We have had an introduction to probability. In the last session we saw how probability is about chance.
You can say: "What is the chance that something will happen?" This is the same
assaying: "What is the probability of something happening?"
It's the same thing really.
Today we are going extend the concept of probability and get you used to using it.
Let us remind ourselves about the chance, or probability, of something happening. It could be:
impossible, certain or somewhere in-between.
If it might happen it could be unlikely, an even chance or likely.
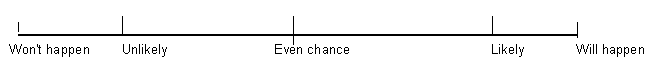
What is the chance of tossing a head or tail on a one pence piece? Where would you put your mark on the line above?
Even chance.
The reason is that there are only two choices so it must be heads or tails.
So the chance of getting a head is 1/2. What is the chance of getting a tail?
Answer: it is 1/2 If we add up both the chances 1/2 + 1/2 = 1.
(This is an important idea in probability, we will come back to it).
The chance of getting a head or a tail is equal, they are both 1/2
So in the coin example we have equal probabilities.
Let us look at a more difficult idea with equal probabilities.
We have asked before: What is the probability that you will draw a red card out of a normal pack of cards with no jokers?
Well you have to know how many cards there are in a normal pack (52)
You have to know how many cards are red (26)
Now you can work out the chance of getting a red card
26 out of 52 or
An even chance since 26/52 = 1/2.
What is the Probability of pulling out a black card and is it an equal probability?
Answer
The chance of pulling out a black card is 26/52 and yes it is an equal probability.
26/52 for red: 26/52 for black
or 1/2 red, 1/2 black = 1 whole one or 1
Again these probabilities add up to one
Remember
This is the basic idea of probability.
How many are there in total and what is your chance of getting your
choice?
We will build on equal probabilities and probabilities adding to one with this last point.

On a normal dice we have the numbers 1 to 6.
What is the chance of throwing a 6?
Remember
How many are there in total and what is your chance of getting your choice?
There are 6 choices, you want one of
them, so the answer is 1/6 (one out of 6)
What are the chances of throwing a 2, 3, 5, or 1?
Answer
In each case the answer is 1/6
If we throw a dice, what is the chance that we won't throw a 4?
Go to answer
Answer
The answer is 5/6 Do you know why?
The question asked what is the chance that we WON'T throw a 4? Since the chance of getting a 4 is 1/6 the chance of not getting a 4 must be 5/6 because 1/6 + 5/6 = 6/6 = 1
Remember, probabilities add up to 1
Finally let us see how powerful this idea is. Try these next questions to finish off for today.
In a bag I have a number of balls, some are red and some are blue.
If the probability of pulling out a red ball is 1/5
A. What is the probability of pulling out a blue ball?
B. If there are 10 balls in the bag. How many are red?
Go to answer
Answer
A. The probability of pulling out a blue ball must be 4/5 (since pulling the red is 1/5 and 1/5 +4/5 =1)
B. The answer is 2 balls are red. (this is because for every 5 balls 1 is red. So for 10 balls there must be 2 red
Review
That was our second look at probability.
Today we looked at:
The basic idea of probability.
How many are there in total and what is your chance of getting your choice?
Equal probabilities (i.e. the chances of something happening being the same for all)
Heads and tails both being 1/2 and throwing a number on a dice, each number being 1/6
All probabilities totalling 1
If the probability of getting something is 1/3, the chance of not getting it is 2/3: 1/3 + 2/3 = 1
Well, that concludes our look at equal probabilities.
Next time we will look at unequal probabilities.
That wasn't too bad was it?
Good Luck!